The search for the source of inspiration in science, mathematics, and art
leads beyond the mechanistic framework of present-day biological theory.
SADAPUTA DASA studied at the State University of New York and Syracuse University and later received a National Science Fellowship. He went on to complete his Ph.D. in mathematics at Cornell, specializing in probability theory and statistical mechanics.

In this article we will examine how human beings acquire knowledge in science, mathematics, and art. Our focus shall primarily be on the formation of ideas and hypotheses in science and mathematics, since the formal nature of these subjects tends to put the phenomena we are concerned with into particularly clear perspective. We will show that the phenomenon known as inspiration plays an essential part in acquiring knowledge in modern science and mathematics and the creative arts (such as music). We will argue that the phenomenon of inspiration can not readily be explained by mechanistic models of nature consistent with present-day theories of physics and chemistry. As an alternative to these models, a theoretical framework for a nonmechanistic description of nature will be outlined. While providing a direct explanation of inspiration, this general framework is broad enough to include the current theories of physics as a limiting case.
Modern scientists acquire knowledge, at least in principle, by what is called the hypothetico-deductive method. Using this method, they formulate hypotheses and then test them by experimental observation. Investigators consider the hypotheses valid only insofar as they are consistent with the data obtained by observation, and they must in principle reject any hypothesis that disagrees with observation. Much analysis has been directed toward the deductive side of the hypotheticodeductive method, but the equally important process of hypothesis formation has been largely neglected. So we ask, "Where do the hypotheses come from?"
It is clear that scientists cannot use any direct, step-by-step process to derive hypothesis from raw observational data. To deal with such data at all, they must already have some working hypothesis, for otherwise the data amounts to nothing more than a bewildering array of symbols (or sights and sounds), which is no more meaningful than a table of random numbers. In this connection Albert Einstein once said, "It may be heuristically useful to keep in mind what one has observed. But on principle it is quite wrong to try grounding a theory on observable magnitudes alone. In reality the very opposite happens. It is the theory which determines what we can observe." ** (S. G. Brush, "Should the History of Science Be Rated X?" Science, Vol. 183, p. 1167.)
Pure mathematics contains an equivalent of the hypothetico-deductive method. In this case, instead of hypotheses there are proposed systems of mathematical reasoning intended to answer specific mathematical questions. And instead of the experimental testing of a hypothesis there is the step-by-step process of verifying that a particular proof, or line of mathematical reasoning, is correct. This verification process is straightforward and could in principle be carried out by a computer. However, there is no systematic, step-by-step method of generating mathematical proofs and systems of ideas, such as group theory or the theory of Lebesque integration.
If hypotheses in science and systems of reasoning in mathematics are not generated by any systematic procedure, then what is their source? We find that they almost universally arise within the mind of the investigator by sudden inspiration. The classic example is Archimedes' discovery of the principle of specific gravity. The Greek mathematician was faced with the task of determining whether a king's crown was solid gold without drilling any holes in it. After a long period of fruitless endeavor, he received the answer to the problem by sudden inspiration while taking a bath.
Such inspirations generally occur suddenly and unexpectedly to persons who had previously made some unsuccessful conscious effort to solve the problem in question. They usually occur when one is not consciously thinking about the problem, and they often indicate an entirely new way of looking at it a way the investigator had never even considered during his conscious efforts to find a solution. Generally, an inspiration appears as a sudden awareness of the problem's solution, accompanied by the conviction that the solution is correct and final. One perceives the solution in its entirety, though it may be quite long and complicated when written out in full.
Inspiration plays a striking and essential role in the solution of difficult problems in science and mathematics. Generally, investigators can successfully tackle only routine problems by conscious endeavor alone. Significant advances in science almost always involve sudden inspiration, as the lives of great scientists and mathematicians amply attest. A typical example is the experience of the nineteenth-century mathematician Karl Gauss. After trying unsuccessfully for years to prove a certain theorem about numbers, Gauss suddenly became aware of the solution. He described his experience as follows: "Finally, two days ago, I succeeded. . . . Like a sudden flash of lightning, the riddle happened to be solved. I myself cannot say what was the conducting thread which connected what I previously knew with what made my success possible:" ** (J. Hadamard, The Psychology of Invention in the Mathematical Field (Princeton: Princeton University Press, 1949), p. 15.)

Karl Gauss
We can easily cite many similar examples of sudden inspiration. Here is another one, given by Henri Poincarb, a famous French mathematician of the late nineteenth century. After working for some time on certain problems in the theory of functions, Poincarb had occasion to go on a geological field trip, during which he set aside his mathematical work. While on the trip he received a sudden inspiration involving his researches, which he described as follows: "At the moment when I put my foot on the step the idea came to me, without anything in my former thoughts seeming to have paved the way for it, that the transformations I had used . . . were identical with those of non-Euclidean geometry." ** (Henri Poincare, The Foundations of Science (Lancaster, Pa.: The Science Press, 1946), pp. 387-8.) Later on, after some fruitless work on an apparently unrelated question, he suddenly realized, "with just the same characteristics of brevity, suddenness, and immediate certainty," ** (Ibid.) that this work could be combined with his previous inspiration to provide a significant advance in his research on the theory of functions. Then a third sudden inspiration provided him with the final argument he needed to complete that work.
Although inspirations generally occur after a considerable period of intense but unsuccessful effort to consciously solve a problem, this is not always the case. Here is an example from another field of endeavor. Wolfgang Mozart once described how he created his musical works: "When I feel well and in good humor, or when I am taking a drive or walking…. thoughts crowd into my mind as easily as you could wish. Whence and how do they come? I do not know and I have nothing to do with it…. Once I have a theme, another melody comes, linking itself with the first one, in accordance with the needs of the composition as a whole…. Then my soul is on fire with inspiration, if however nothing occurs to distract my attention. The work grows; I keep expanding it, conceiving it more and more clearly until I have the entire composition finished in my head, though it may be long…. It does not come to me successively, with its various parts worked out in detail, as they will be later on, but it is in its entirety that my imagination lets me hear it." ** (Hadamard, op. cit., p. 16.) (Italics added.)
From these instances we discover two significant features of the phenomenon of inspiration: first, its source lies beyond the subject's conscious perception; and second, it provides the subject with information unobtainable by any conscious effort. These features led Poincare and his follower Hadamard to attribute inspiration to the action of an entity which Poincare called "the subliminal self," and which he identified with the subconscious or unconscious self of the psychoanalysts. Poincare came to the following interesting conclusions involving the subliminal self: "The subliminal self is in no way inferior to the conscious self; it is not purely automatic; it is capable of discernment; it has tact, delicacy; it knows how to choose, to divine. What do I say? It knows better how to divine than the conscious self, since it succeeds where that has failed. In a word, is not the subliminal self superior to the conscious self?" ** (Poincare, op. cit., p. 390.) Having raised this question, Poincare then backs away from it: "Is this affirmative answer forced upon us by the facts I have just given? I confess that for my part, I should hate to accept it." ** (Ibid., p. 391.) He then offers a mechanical explanation of how the subliminal self, viewed as an automaton, could account for the observed phenomena of inspiration.
The Mechanistic Explanation
Let us carefully examine the arguments for such a mechanical explanation of inspiration. This question is of particular importance at the present time, because the prevailing materialistic philosophy of modern science holds that the mind is nothing more than a machine, and that all mental phenomena, including consciousness, are nothing more than the products of mechanical interactions. The mental machine is specifically taken to be the brain, and its basic functional elements are believed to be the nerve cells and possibly some systems of interacting macro- molecules within these cells. Many modern scientists believe that all brain activity results simply from the interaction of these elements according to the known laws of physics.

Wolfgang Mozart
No one (as far as we are aware) has yet formulated an adequate explanation of the difference between a conscious and an unconscious machine, or even indicated how a machine could be conscious at all. In fact, investigators attempting to describe the self in mechanistic terms concentrate exclusively on the duplication of external behavior by mechanical means; they totally disregard each individual person's subjective experience of conscious self-awareness. This approach to the self is characteristic of modern behavioral psychology. It was formally set forth by the British mathematician A. M. Turing, who argued that since whatever a human being can do a computer can imitate, a human being is merely a machine.
For the moment we will follow this behavioristic approach and simply consider the question of how the phenomenon of inspiration could be duplicated by a machine. Poincare proposed that the subliminal self must put together many combinations of mathematical symbols by chance until at last it finds a combination satisfying the desire of the conscious mind for a certain kind of mathematical result. He proposed that the conscious mind would remain unaware of the many useless and illogical combinations running through the subconscious, but that it would immediately become aware of a satisfactory combination as soon as it was formed. He therefore proposed that the' subliminal self must be able to form enormous numbers of combinations in a short time, and that these could be evaluated subconsciously as they were formed, in accordance with the criteria for a satisfactory solution determined by the conscious mind.
As a first step in evaluating this model, let us estimate the number of combinations of symbols that could be generated within the brain within a reasonable period of time. A very generous upper limit on this number is given by the figure 3.2 X 10(46). We obtain this figure by assuming that in each cubic Angstrom unit of the brain a separate combination is formed and evaluated once during each billionth of a second over a period of one hundred years. Although this figure is an enormous overestimate of what the brain could possibly do within the bounds of our present understanding of the laws of nature, it is still infinitesimal compared to the total number of possible combinations of symbols one would have to form to have any chance of hitting a proof for a particular mathematical theorem of moderate difficulty.
If we attempt to elaborate a line of mathematical reasoning, we find that at each step there are many possible combinations of symbols we can write down, and thus we can think of a particular mathematical argument as a path through a tree possessing many successive levels of subdividing branches. This is illustrated in the figure at right. The number of branches in such a tree grows exponentially with the number of successive choices, and the number of choices is roughly proportional to the length of the argument. Thus as the length of the argument increases, the number of branches will very quickly pass such limits as 10(46) and 10(100) (1 followed by 100 zeros). For example, suppose we are writing sentences in some symbolic language, and the rules of grammar for that language allow us an average of two choices for each successive symbol. Then there will be approximately 10 grammatical sentences of 333 symbols in length.
Even a very brief mathematical argument will often expand to great length when written out in full, and many mathematical proofs require pages and pages of highly condensed exposition, in which many essential steps are left for the reader to fill in. Thus there is only an extremely remote chance that an appropriate argument would appear as a random combination in Poincare's mechanical model of the process of inspiration. Clearly, the phenomenon of inspiration requires a process of choice capable of going more or less directly to the solution, without even considering the vast majority of possible combinations of arguments.
Some Striking Examples
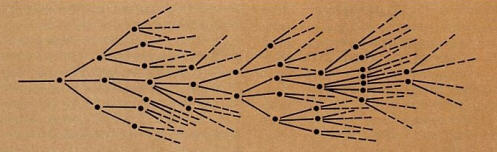
The requirements that this process of choice must meet are strikingly illustrated by some further examples of mathematical inspiration. It is very often found that the solution to a difficult mathematical problem depends on the discovery of basic principles and underlying systems of mathematical relationships. Only when these principles and systems are understood does the problem take on a tractable form; therefore difficult problems have often remained unsolved for many years, until mathematicians gradually developed various sophisticated ideas and methods of argument that made their solution possible. However, it is interesting to note that on some occasions sudden inspiration has completely circumvented this gradual process of development. There are several instances in which famous mathematicians have, without proof, stated mathematical results that later investigators proved only after elaborate systems of underlying relationships had gradually come to light. Here are two examples:
The first example concerns the zeta-function studied by the German mathematician Bernhard Riemann. At the time of his death, Riemann left a note describing several properties of this function that pertained to the theory of prime numbers. He did not indicate the proof of these properties, and many years elapsed before other mathematicians were able to prove all but one of them. The remaining question is still unsettled, though an immense amount of labor has been devoted to it over the last seventy-five years. Of the properties of the zeta-function that have been verified, the mathematician Jacques Hadamard said, "All these complements could be brought to Riemann's publication only by the help of facts which were completely unknown in his time; and, for one of the properties enunciated by him, it is hardly conceivable how he can have found it without using some of these general principles, no mention of which is made in his paper." ** (Hadamard, op. cit., p. 118.)
The work of the French mathematician Evariste Galois provides us with a case similar to Riemann's. Galois is famous for a paper, written hurriedly in sketchy form just before his death, that completely revolutionized the subject of algebra. However, the example we are considering here concerns a theorem Galois stated, without proof, in a letter to a friend. According to Hadamard this theorem could not even be understood in terms of the mathematical knowledge of that time; it became comprehensible only years later, after the discovery of certain basic principles. Hadamard remarks "(1) that Galois must have conceived these principles in some way; (2) that they must have been unconscious in his mind, since he makes no allusion to them, though they by themselves represent a significant discovery." ** (Ibid., p. 120.)
It would appear, then, that the process of choice underlying mathematical inspiration can make use of basic principles that are very elaborate and sophisticated and that are completely unknown to the conscious mind of the person involved. Some of the developments leading to the proof of some of Riemann's theorems are highly complex, requiring many pages (and even volumes) of highly abbreviated mathematical exposition. It is certainly hard to see how a mechanical process of trial and error, such as that described by Poincare, could exploit such principles. On the other hand, if other, simpler solutions exist that avoid the use of such elaborate developments, they have remained unknown up to the present time, despite extensive research devoted to these topics.
The process of choice underlying mathematical inspiration must also make use of selection criteria that are exceedingly subtle and hard to define. Mathematical work of high quality cannot be evaluated simply by the application of cut-and-dried rules of logic. Rather, its evaluation involves emotional sensibility and the appreciation of beauty, harmony, and other delicate aesthetic qualities. Of these criteria Poincare said, "It is almost impossible to state them precisely; they are felt rather than formulated." ** (Poincare, op. cit., p. 390.) This is also true of the criteria by which we judge artistic creations, such as musical compositions. These criteria are very real but at the same time very difficult to define precisely. Yet evidently they were fully incorporated in that mysterious process which provided Mozart with sophisticated musical compositions without any particular effort on his part and, indeed, without any knowledge of how it was all happening.
If the process underlying inspiration is not one of extensive trial and error, as Poincare suggested, but rather one that depends mainly on direct choice, then we can explain it in terms of current mechanistic ideas only by positing the existence of a very powerful algorithm (a system of computational rules) built into the neural circuitry of the brain. However, it is not at all clear that we can satisfactorily explain inspiration by reference to such an algorithm. Here we will only briefly consider this hypothesis before going on to outline an alternative theoretical basis for the understanding of inspiration.
The brain-algorithm hypothesis gives rise to the following basic questions:
(1) Origins. If mathematical, scientific, and artistic inspirations result from the workings of a neural algorithm, then how does the pattern of nerve connections embodying this algorithm arise? We know that the algorithm cannot be a simple one when we consider the complexity of automatic theorem-proving algorithms that have been produced thus far by workers in the field of artificial intelligence. ** (Joseph Weizenbaum, Computer Power and Human Reason (San Francisco: W. H. Freeman & Company, 1976), ch. 9.) These algorithms cannot even approach the performance of advanced human minds, and yet they are extremely elaborate. But if our hypothetical brain-algorithm is extremely complex, how did it come into being? It can hardly be accounted for by extensive random genetic mutation or recombination in a single generation, for then the problem of random choice among vast numbers of possible combinations would again arise. One would therefore have to suppose that only a few relatively probable genetic transformations separated the genotype of Mozart from those of his parents, who, though talented, did not possess comparable musical ability.
However, it is not the general experience of those who work with algorithms that a few substitutions or recombinations of symbols can drastically improve an algorithm's performance or give it completely new capacities that would impress us as remarkable. Generally, if this were to happen with a particular algorithm, we would tend to suppose that it was a defective version of another algorithm originally designed to exhibit those capacities. This would imply that the algorithm for Mozart's unique musical abilities existed in a hidden form in the genes of his ancestors.
This brings us to the general problem of explaining the origin of human traits. According to the theory most widely accepted today, these traits were selected on the basis of the relative reproductive advantage they conferred on their possessors or their possessors' relatives. Most of the selection for our hypothetical hidden algorithms must have occurred in very early times, because of both the complexity of these algorithms and the fact that they are often carried in a hidden form. It is now thought that human society, during most of its existence, was on the level of hunters and gatherers, at best. It is quite hard to see how, in such societies, persons like Mozart or Gauss would ever have had the opportunity to fully exhibit their unusual abilities. But if they didn't, then the winnowing process that is posited by evolution theory could not effectively select these abilities.
We are thus faced with a dilemma: It appears that it is as difficult to account for the origin of our hypothetical inspirationgenerating algorithms as it is to account for the inspirations themselves.
(2) Subjective experience. If the phenomenon of inspiration is caused by the working of a neural algorithm, then why is it that an inspiration tends to occur as an abrupt realization of a complete solution, without the subject's conscious awareness of intermediate steps? The examples of Riemann and Galois show that some persons have obtained results in an apparently direct way, while others were able to verify these results only through a laborious process involving many intermediate stages. Normally, we solve relatively easy problems by a conscious, step-by-step process. Why, then, should inspired scientists, mathematicians, and artists remain unaware of important intermediate steps in the process of solving difficult problems or producing intricate works of art, and then become aware of the final solution or creation only during a brief experience of realization?
Thus we can see that the phenomenon of inspiration cannot readily be explained by means of mechanistic models of nature consistent with present-day theories of physics and chemistry. In the remainder of this article we will suggest an alternative to these models.
An Alternative Model
It has become fairly commonplace for scientists to look for correspondence between modern physics and ancient Eastern thought, and to find intriguing suggestions for hypotheses in the Upanisads, the Bhagavad-gita, and similar Vedic texts. TheBhagavad-gita in particular gives a description of universal reality in which the phenomenon of inspiration falls naturally into place. Using some fundamental concepts presented in the Bhagavad-gita, we shall therefore outline a theoretical framework for the description of nature that provides a direct explanation of inspiration, but that is still broad enough to include the current theories of physics as a limiting case. Since here we are offering these concepts only as subject matter for thought and discussion, we will not try to give a final of rigorous treatment.
The picture of universal reality presented in the Bhagavad-gita differs from that of current scientific thinking in two fundamental respects:
(1) Consciousness is understood to be a fundamental feature of reality rather than a by-product of the combination of nonconscious entities.
(2) The ultimate causative principle underlying reality is understood to be unlimitedly complex, and to be the reservior of unlimited organized forms and activities. Specifically, the Bhagavad-gita posits that the underlying, absolute cause of all causes is a universal conscious being, and that the manifestations of material energy are exhibitions of that being's conscious will. The individual subjective selves of living beings (such as ourselves) are understood to be minute parts of the absolute being that possess the same self-conscious nature. These minute conscious selves interact directly with the absolute being through consciousness, and they interact indirectly with matter through the agency of the absolute being's control of matter.
In modern science the idea of an ultimate cause underlying the phenomenal manifestation is expressed through the concept of the laws of nature. Thus in modern physics all causes and effects are thought to be reducible to the interaction of fundamental physical entities, in accordance with basic force laws. At the present moment the fundamental entities are thought by some physicists to comprise particles such as electrons, muons, neutrinos, and quarks, and the force laws are listed as strong, electromagnetic, weak, and gravitational. However, the history of science has shown that it would be unwise to consider these lists final. In the words of the physicist David Bohm, "The possibility is always open that there may exist an unlimited variety of additional properties, qualities, entities, systems, levels, etc., to which apply correspondingly new kinds of laws of nature." ** (David Bohm, Causality and Chance in Modern Physics (London: Routledge and Kegan Paul Ltd., 1957), p. 133.)
The picture of reality presented in the Bhagavad-gita could be reconciled with the world-view of modern physics if we were to consider mathematical descriptions of reality to be approximations, at best. According to this idea, as we try to formulate mathematical approximations closer and closer to reality, our formalism will necessarily diverge without limit in the direction of ever-increasing complexity. Many equations will exist that describe limited aspects of reality to varying degrees of accuracy, but there will be no single equation that sums up all principles of causation.
We may think of these equations as approximate laws of nature, representing standard principles adopted by the absolute being for the manifestation of the physical universe. The Bhagavad-gita describes the absolute being in apparently paradoxical terms, as simultaneously a single entity and yet all-pervading in space and time. This conception, however, also applies to the laws of physics as scientists presently understand them, for each of these laws requires that a single principle (such as the principle of gravitational attraction with the universal constant G) apply uniformly throughout space and time.
The difference between the conceptions of modern physics and those presented in the Bhagavad-gita lies in the manner in which the ultimate causal principle exhibits unity. The goal of many scientists has been to find some single, extremely simple equation that expresses all causal principles in a unified form. According to the Bhagavad-gita, however, the unity of the absolute being transcends mathematical description. The absolute being is a single self-conscious entity possessing unlimited knowledge and potency. Therefore a mathematical account of this being would have to be limitlessly complex.
According to the Bhagavad-gita, the phenomenon of inspiration results from the interaction between the all-pervading absolute being and the localized conscious selves. Since the absolute being's unlimited potency is available everywhere, it is possible for all varieties of artistic and mathematical creations to directly manifest within the mind of any individual.
These creations become manifest by the will of the absolute being in accordance with both the desire of the individual living being and certain psychological laws.
Conclusion
We have observed that the attempt to give a mechanical explanation of inspiration based on the known principles of physics meets with two fundamental difficulties. First, the process of inspiration can be explained mechanically only if we posit the existence of an elaborate algorithm embodied in the neural circuitry of the brain. However, it is as hard to account for the origin of such an algorithm as it is to account for the inspirations themselves. Second, even if we accept the existence of such an algorithm, the mechanical picture provides us with no understanding of the subjective experience of inspiration, in which a person obtains the solution to a problem by sudden revelation, without any awareness of intermediate steps.
If it is indeed impossible to account for inspiration in terms of known causal principles, then it will be necessary to acquire some understanding of deeper causal principles operating in nature. Otherwise, no explanation of inspiration will be possible. It is here that the worldview presented in the Bhagavad-gita might be useful to investigators. The Bhagavad-gita provides a detailed account of the laws by which the individual selves and the absolute being interact, and this account can serve as the basis for a deeper investigation of the phenomenology of inspiration.
